Dimensionless Numbers In Heat Transfer
In
Heat Transfer, Dimensionless numbers are
used to characterize and classify heat transfer problems. This blog attempts to
explain the meaning and significance of these numbers and help you to get used
to them.
Introduction:
Dimensionless
numbers are scalar quantities commonly used in fluid mechanics and heat
transfer analysis to study the relative strengths of inertial, viscous,
thermal, and mass transport forces in a system.
Dimensionless
numbers are equal for dynamically similar systems, systems with the same
geometry, and boundary conditions. This makes them a powerful tool for scaling
operations from model to pilot and beyond. It helps in determining
a systematic arrangement of the variables in the physical relationship.
Importance of
Dimensionless Number:
We can experiment
with model automobiles, planes, and ships and make predictions about how the
big thing will behave in real-world scenarios thanks to dimensionless numbers.
All that needs to be done is to confirm that the model and the real thing are
similar.
Why Dimensionless
Numbers used in Heat Transfer:
- Dimensionless numbers allow for comparisons between very different systems.
- Dimensionless numbers tell you how the system will behave.
- Many useful relationships exist between dimensionless numbers that tell you how specific things influence the system.
- Dimensionless numbers allow you to solve a problem more easily.
- When we need to solve a problem numerically, dimensionless groups help you to scale your problem.
1.
Reynolds Number:
It is defined as the ratio of the inertia force to viscous force.
where
·
U flow Speed
· L
characteristic length
· υ kinematic viscosity
Significance:
· Reynolds number signifies the relative importance of the inertia to the viscous forces occurring in the flow systems.
· The higher the value of Re the greater will be the relative contribution of inertia effect. The smaller the value of Re, the greater will be the relative magnitude of the viscous stresses.
· Reynolds number is taken as an important criterion of kinematic and dynamic similarities in forced convection heat transfer.
2.
Prandtl Number:
It is named after
Ludwig Prandtl, who introduced the concept of boundary layer in 1904 and made
significant contributions to boundary layer theory.
Prandtl Number is the ratio of kinematic viscosity to thermal diffusivity of
the fluid. It tells about relative importance between the momentum diffusivity
to the thermal diffusivity.
where
- υ is momentum diffusivity
(m2/s)
- α is thermal diffusivity
(m2/s)
- μ is dynamic viscosity
(N.s/m2)
- K is thermal
conductivity (W/m. k)
- cp is
specific heat (J/kg. k)
- ρ is density (kg/m3)
Significance:
- Prandtl number provides a
measure of the relative effectiveness of the momentum and energy transport
by diffusion.
- Prandtl number is a
connecting link between the velocity field and temperature field, and its
value strongly influences relative growth of velocity and thermal boundary
layers.
- Solely on fluid and its
characteristics.
- It is the proportion of a
fluid’s momentum to heat diffusivity.
- Additionally, it is the
proportion of thermal to velocity boundary layers.
- Prandtl number is a
connecting link between the velocity field and temperature field, and its
value strongly influences relative growth of velocity and thermal boundary
layers.
- Prandtl number is dependent on
dynamic viscosity. By increasing dynamic viscosity Prandtl number also increases.
3.
Grashof Number:
Grashof Number indicates the relative dominance of
inertia and buoyant forces over viscous force. It is defined as the ratio of
the product of inertia force and buoyancy force to the square of viscous force.
Grashof number is related with natural convection heat transfer.
Where
- g is the acceleration
due to Earth’s gravity,
- β is the coefficient of
thermal expansion,
- Ts is the
wall temperature
- T∞ is
the bulk temperature,
- L is the vertical
length,
- ν is the kinematic
viscosity
Significance:
·
The ratio of natural convection’s buoyancy and viscous forces.
·
Grashof number is used in natural convection, the
Reynolds number is used in forced convection of fluid flow.
4.
Nusselt Number:
Nu established the
relation between convective film coefficient
(h), thermal conductivity of the fluid (K) and a significant length. It is the ratio of
heat flow rate by convection process under a unit temperature gradient to the
heat flow rate by conduction process under a unit temperature gradient through
a stationary thickness of L metres.
where
- kf is
the thermal conductivity of the fluid [W/m. K]
- L is
the characteristic length
- h is the convective
heat transfer coefficient (W/m2. K)
Significance:
· The ratio of the boundary layer’s
convective to conductive heat transfer coefficient.
·
Low Nu results in increased
conduction and laminar flow.
·
High Nu = more convection = turbulent
flow.
·
It can also be seen as the material’s
conduction resistance to convection resistance.
·
Nu = f(Re, pr)
·
It represent dimensionless heat
transfer coefficient.
5.
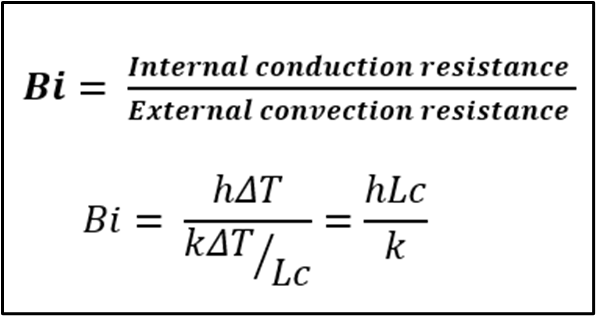
Biot Number:
The Biot number
is the ratio of the internal resistance of a body to heat conduction to its
external resistance to heat convection. Therefore, a small Biot number
represents small resistance to heat conduction, and thus small temperature
gradients within the body.
where
- k thermal conductivity
of the body
- h convective heat
transfer coefficient
- L characteristic length
(m) (Volume/Total Surface Area)
Significance:
·
It is used when there is a transient
(unsteady state) heat transfer.
·
The ratio of the body’s internal heat
transfer resistance to its external heat transfer resistance exterior thermal
resistance divided by internal thermal resistance.
·
When the body’s internal heat
transfer resistance is less than 0.1, conduction occurs more quickly than
convection at the surface.
·
It is use in unsteady heat transfer.
6.
Rayleigh Number:
Rayleigh number
is the product of the Grashof and Prandtl numbers.
Where
- g is the acceleration
due to Earth’s gravity,
- β is the coefficient of
thermal expansion,
- Ts is the
wall temperature
- T∞ is
the bulk temperature,
- L is the vertical
length,
- ν is the kinematic viscosity
· It number plays an
important role in determining whether natural convection flow is laminar or
turbulent.
7.
Fourier Number:
The Fourier number is a measure of
heat conducted through a body relative to heat stored.
where
- α = Thermal
diffusivity
- t = Time (in Second)
- Lc =
Characteristics length
Significance:
·
The ratio of the rate of heat storage
to the rate of heat rate of heat conduction.
·
A large value of the Fourier number
indicates faster propagation of heat through a body.
·
Used in conjunction with the Biot
number to solve heat transport problems in transient states.
·
The Fourier number for MT is utilized
for mass transfer by diffusion.
·
It can also be thought of as the
interval from the present to the time required to reach a steady state.
· It represent dimensionless time
Conclusion:
Dimensionless
numbers play an important role in analysing fluid dynamics and heat and mass
transfer problems. They provide a method by which complex phenomena can be
characterized, often by way of a simple, single-number comparison. It gives the
relationship of Heat Transfer with Mass Transfer and Fluids Mechanics.
References
1.
Heat Transfer, A Practical Approach, Yunus A. Dengel, Mcgraw-Hills
2. Heat and Mass Transfer, R.K.
Rajput, S. Chand
3.
A Heat TransferTextbook, by John H. Lienhard IV and John H. Lienhard
V
Published By:-
Prof. Avadhoot Rajurkar
(54) Swarada Kulkarni
(58) Jayesh Mane
(63) Sakshi Niphade
(76) Aditya Rathod
(77) Darshan Rathod



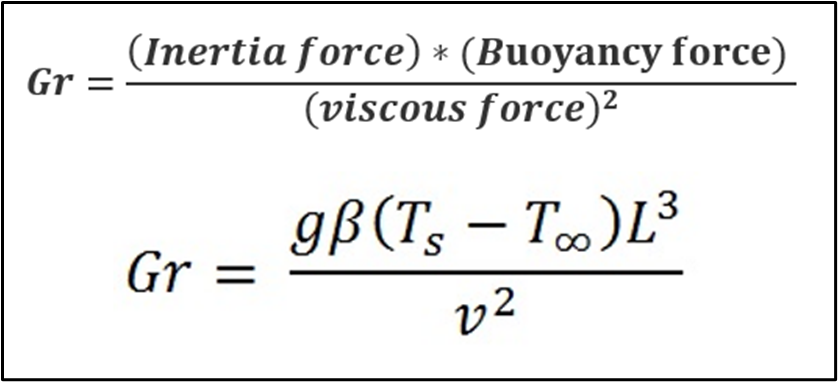




Well defined concepts!!
ReplyDeleteInformative Blog
ReplyDelete